Magnetization dynamics in magnetic media
Keywords:
Dynamical systems, fase map, magnetization, magnetic mediaAbstract
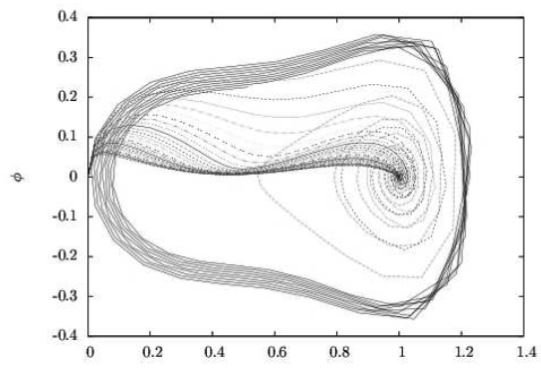
This work is a study of magnetization evolution in magnetic media along the time. The magnetic media is a flat tape, like a tape use for record and tape information, with effective field including first order term from cubic net, uniaxial anisotropics fields, demagnetized field and interchange term between the net elements. The magnetization is driven from the demagnetized to the magnetized state by a dc applied magnetic fiel.The theoretical model show a solution of a Landau-Lifshitz-Gilbert equation, taking into account the speed of the tape. Four physicaly admisible solution are obtained: harmonic oscillations, damped oscillation, exponential fronts and double exponential fronts, for a different parameter values. We show an approximation to the problem from the dynamical system theory, when the equation is converted into a non-time depending autonomous system, for study the existence of fix points, the transition between solutions and the phase map of the solutions and his physical interpretation. The different phase map are presented for representative sets of values. This approximation to the problem complements and enriches the previous works.
Downloads
References
Cand`es, E., y Recht, B. (2009). Exact matrix completion via convex optimization. Foundations of Computational Mathematics, 9(6), 717-772.
Chen, M., Lin, Z., y Ma, Y. (2010). The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv preprint arXiv:1009.5055.
Delyon, B., Lavielle, M., y Moulines, E. (1999). Convergence of a stochastic approximation version of the em algorithm. The Annals of Statistics, 27(1), 94-128.
Dempster, A., Laird, N., y Rubin, D. (1977). Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society. Series B (Methodological)., 39(1), 1- 38.
Hassan, R. (2009). Problemas de completaci´on de matrices parcia- les (Tesis Doctoral no publicada). Universidad Polit´ecnica de Valencia.
Kuhn, E., y Lavielle, M. (2004). Coupling a stochastic approximation version of em with an mcmc procedure. ESAIM: Probability and Statistics, 9, 115-131.
Lara, H., Oviedo, H., y Yuan, J. (2014). Matrix completion via a low rank factorization model and an augmented lagrangean succesive overrelaxation algorithm. CompAMa, 2(2), 21-46.
Lawrence, N., y Urtasun, R. (2009). Non-linear matrix factorization with gaussian processes. En Proceedings of the 26th annual international conference on machine learning (pp. 601–608).
L´eger, F., Yu, G., y Sapiro, G. (2010). Efficient matrix completion with gaussian models. arXiv preprint arXiv:1010.4050.
Salakhutdinov, R., y Mnih, A. (2008a). Bayesian probabilistic matrix factorization using markov chain monte carlo. Proceedings of the International Conference in Machine Learning. ACM, 880- 887.
Salakhutdinov, R., y Mnih, A. (2008b). Probabiltic matrix factorization. Advances in neural information processing systems, 1257-1264.
Wen, Z., Yin, W., y Zhang, Y. (2012). Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Mathematical Programming Compu- tation, 4(4), 333–361.
Published
How to Cite
Issue
Section
Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0)
The opinions expressed by the authors do not necessarily reflect the position of the publisher of the publication or of UCLA. The total or partial reproduction of the texts published here is authorized, as long as the complete source and the electronic address of this journal are cited.
The authors fully retain the rights to their works, giving the journal the right to be the first publication where the article is presented. The authors have the right to use their articles for any purpose as long as it is done for non-profit. Authors are recommended to disseminate their articles in the final version, after publication in this journal, in the electronic media of the institutions to which they are affiliated or personal digital media.
